Latihan Soal Dan Pembahasan Un/Unbk Matematika Smk 2019
Latihan Soal dan Pembahasan UN/UNBK Matematika Sekolah Menengah kejuruan 2019. Hai sahabat kembali lagi dengan admin , Di kesempatan kali ini admin akan menawarkan latihan soal yang dianggap paling sulit untuk anak - anak SMK, yaitu mata pelajaran matematika (TKP, AKP, dan PSP).
Entah sulit alasannya yaitu tidak sanggup melaksanakan kecurangan atau gimana. Karena memang betul sih, berbeda dengan mata ujian lainnya yang dimana sanggup tanya dengan gampang dengan bermodalkan petunjuk biasa.
Di mata Ujian UNBK matematika Sekolah Menengah kejuruan setiap soalnya harus memakai rumus rumus yang bakal menciptakan sahabat merasa kesulitan terhadap setiap butirnya. Tapi sebagai anak SMK, niscaya nemu caranya sih. Wkwkwkwk
Oleh alasannya yaitu itulah admin menawarkan contoh latihan soal un matematika SMK ini untuk sahabat jadikan prediksi ihwal apa yang akan diujikan pada Ujian Nasional tahun pelajaran 2018/2019.
UNBK aja sih ya menyebutnya. Kalau UN akhirnya cuma sekedar Ujian Nasional saja. Kalau UNBK sendiri sudah memakai komputer sebagai sistem Ujiannya.
Di Sekolah Menengah kejuruan sendiri untuk tahun depan akan diberlangsungkan UNBK secara menyeluruh. Didukung juga dengan sistem Resource Sharing, yang dimana sekolah lain sanggup menumpang untuk melaksanakan sistem tersebut.
Latihan Soal dan Pembahasan UN/UNBK Matematika Sekolah Menengah kejuruan 2019
Berbeda dengan soal lainnya di Blog soalprediksi.com. Pada mata pelajaran Matematika ini admin hanya menyediakan latihan soal online tanpa adanya dokumen PDF di dalamnya. Dan untuk copy paste untuk keperluan blog sahabat tidak diijinkan.
Selamat mengerjakan Latihan Soal dan Pembahasan UN Matematika Sekolah Menengah kejuruan 2019
1. Untuk menciptakan 1.500 unit barang dengan menggunakan mesin tertentu dibutuhkan waktu selama 30 jam. Banyak barang yang sanggup dibentuk dengan memakai mesin
yang sama dalam waktu 24 jam yaitu . . . .
A. 900 unit
B. 1.050 unit
C. 1.100 unit
D. 1.150 unit
E. 1.200 unit
3. Bentuk sederhana dari (√3 - 2) (√3 + 5) adalah ....
A. 1 - 2√3
A. 900 unit
B. 1.050 unit
C. 1.100 unit
D. 1.150 unit
E. 1.200 unit
Pembahasan Nomor 1
Pembahasan Nomor 2
3. Bentuk sederhana dari (√3 - 2) (√3 + 5) adalah ....
A. 1 - 2√3
B. 3√3 - 7
C. 3 - 2√3
D. 7 - 3√3
E. 7 - √3
Pembahasan Nomor 3
4. Jika 2log 3 = a dan 2log 5 = b, nilai 2log 135 yaitu ....
A. 3(a + b)
B. 3a + b
C. a+ 3b
D. a3 + b
E. a+ b3
5. Untuk membeli 3 benda A dan 4 benda B Ria membayar Rp19.000,00; sedangkan untuk membeli 2 benda A dan 7 benda B Ria membayar Rpl 7.000,00. Jika Ria membeli
4 benda A dan 8 benda B, Ria harus membayar ....
A. Rp 18.000,00
B. Rp 19.500,00
C. Rp 20.000,00
D. Rp24.000,00
E. Rp28.000,00
6. Diketahui persamaan garis 2x - y = 5 dan 3x - y = 2. Persamaan garis yang melalui titik potong kedua garis tersebut dan sejajar garis y - 3x = 2 yaitu ....
A y = 3x + 2
B. y = 3x - 5
C. y = 3x - 2
D. y = 13x + 5
E. y = - 13x - 6
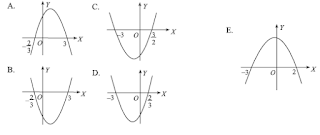
7. Grafik dari fungsi kuadrat f(x)= 3x2 + 7x - 6 yaitu .
B. 3x + 2y < 60; x + 2y < 100; x > 0; y > 0
C. 3x + 2y < 100; x + 2y < 60; x > 0; y > 0
D. 2x + 3y < 60; 2x + 2y < 100; x > 0; y > 0
E. 2x + 3y < 100; 2x + 2y < 60; x > 0; y > 0
9. Daerah yang diarsir pada gambar di samping merupakan penyelesaian suatu sistem pertidaksamaan linear.

Sistem pertidaksamaan linear yang memenuhi adalah
A. x + 4y > 4; 4x + 3y < 12; x > 0; y > 0
B. x + 4y > 4; 3x + 4y < 12; x > 0; y > 0
C. x + 4y < 4; 3x + 4y < 12; x > 0; y > 0
D. 4x + y < 4; 4x + 3y < 12; x > 0; y > 0
E. 4x + y < 4; 3x + 4y < 12; x > 0; y > 0
10. Diketahui sistem pertidaksamaan x + 4y < 14; 3x + 2y < 12; x > 0; y > 0. Nilai maksimum z = 4x + 5y untuk x dan y pada tempat penyelesaian sistem pertidaksamaan tersebut yaitu . . ..
A. 15
B. 16
C. 23
D. 30
E. 56

13. Garis p melalui titik A(2, 4, -2) dan B( 4, 1, -1 ), sedangkan garis q melalui titik C(7, 0, 2) dan D(8, 2, -1). Besar sudut antara garis p dan q yaitu . . . .
A. 0°
B. 45°
C. 60°
D. 120°
E. 135°
Pembahasan Nomor 13
14. Ingkaran dari pemyataan "Jika batas nilai kelulusan tinggi, maka beberapa siswa gagal ujian" yaitu ...
A. Jika batas nilai kelulusan tidak tinggi, maka beberapa siswa lulus ujian.
B. Jika batas nilai kelulusan tidak tinggi, maka beberapa siswa tidak gagal ujian.
C. Jika beberapa siswa tidak gagal ujian, maka batas nilai kelulusan tidak tinggi.
D. Batas nilai kelulusan tinggi tetapi semua siswa tidak gagal ujian.
E. Batas nilai kelulusan tidak tinggi dan semua siswa tidak gagal ujian.
Pembahasan Nomor 14
15. Kontraposisi dari pemyataan: "Jika x2 - 0,04 > 0, maka x < -0,2 atau x > 0,2" yaitu ...
A. Jika x < -0,2 atau x > 0,2, maka x2 - 0,04 > 0.
B. Jika -0,2 < x < 0,2, maka x2 - 0,04 < 0.
C. Jika -0,2 < x < 0,2, maka x2 - 0,04 < 0.
D. Jika x2 - 0,04 < 0, maka -0,2 < x < 0,2.
E. Jika x2 - 0,04 < 0, maka x < -0,2 dan x > 0,2.
16. Diketahui permis-premis sebagai berikut.
Premis 1: Jika seorang siswa kreatif, maka ia akan sekolah di SMK.
Premis 2: Jika seorang siswa sekolah di SMK, maka ia dapat bekerja atau kuliah.
Premis 3: I wan seorang siswa yang tidak bekerja dan tidak kuliah.
Kesimpulan dari premis-premis di atas yaitu ...
A. lwan seorang siswa kreatif.
B. Iwan bukan seorang siswa yang sekolah di SMK.
C. Iwan seorang siswa yang bekerja.
D. Iwan seorang siswa yang sekolah di SMK.
E. Iwan seorang siswa yang tidak kreatif.
17. Perhatikan gambar berikut.

Garis pelukis pada bangkit kerucut di atas ditunjukkan dengan abjad . . . .
A. a
B. b
C. c
D. d
E. e
Pembahasan Nomor 17
18. Perhatikan gambar desain komponen elektro berikut.

Luas permukaan yang tampak pada gambar di atas adalah
A. 98 cm2
B. 116 cm2
c. 175 cm2
D. 224 cm2
E. 274 cm2
Pembahasan Nomor 18
19. Diketahui balok dengan ukuran panjang 20 cm, lebar 15 cm, dan tinggi 8 cm. Luas permukaan balok tersebut adalah ....
A. 240 cm2
B. 320 cm2
C. 600 cm2
D. 1.160 cm2
E. 2.000 cm2
Pembahasan Nomor 19
20. Sebuah tabung tertutup akan dibentuk dari selembar seng dengan jari-jari 28 cm dan tinggi 45 cm. Luas seng yang dibutuhkan untuk menciptakan tabung tersebut yaitu . . . .
A. 4.928 cm2
B. 5.720 cm2
C. 7.920 cm2
D. 9.840 cm2
E. 12.848 cm2
Pembahasan Nomor 20
21. Diketahui prisma dengan bantalan segitiga ketiga sisi berukuran 5 cm, 12 cm, dan 13 cm. Jika tinggi prisma 10 cm, volume prisma tersebut yaitu . . . .
A. 144 cm3
B. 169 cm3
C. 200 cm3
D. 225 cm3
E. 300 cm3
Pembahasan Nomor 21
22. Suatu segitiga ABC dengan panjang sisi AC = 18 cm, B= 60°, dan A = 75°. Panjang sisi AB yaitu ....
A. 3√3
B. 3√6
C. 6√3
D. 6√6
E. 9√6
Pembahasan Nomor 22
23. Koordinat titik P(√24, -2√2) bila diubah ke dalam koordinat polar menjadi ....
A. (4√2, 120°)
B. (4√2, 300°)
C. (4√2, 330°)
D. (6, 300°)
E. (6, 330°)
24. Seorang pengusaha mengurutkan banyak unit barang yang dihasilkannya. Temyata banyak barang yang diproduksi pada tiap bulan sebanyak (25n + 50) unit dengan n
menyatakan bulan (n = 1, 2, 3, ... , 10). Jumlah barang yang diproduksi selama sepuluh bulan yaitu . . ..
A. 2.000 unit
B. 1.950 unit
C. 1.900 unit
D. 1.875 unit
E. 1.825 unit
Pembahasan Nomor 24
25. Jumlah bilangan orisinil antara 1 hingga 100 yang habis dibagi 3 yaitu ....
A. 1.263
B. 1.683
C. 1.789
D. 1.883
E. 1.938
Pembahasan Nomor 25
26. Suku pertama dan kelima dari suatu deret geometri berturut turut adalah 5 dan 80. Jumlah 4 suku pertama dari deret geometri tersebut yaitu . . . .
A. 5
B. 10
C. 25
D. 75
E. 155
Pembahasan Nomor 26
27. Jumlah tak hingga dan suku pertama dari suatu deret geometri berturut-turut yaitu 16 dan 8. Rasio deret tersebut adalah ....
A. 1/4
B. 2/4
C. 3/4
D. 1
E. 5/4
Pembahasan Nomor 27
28. Sebuah nomor rumah terdiri dari tiga angka. Jika angka pertama dan terakhir dari nomor rumah tersebut adalah angka ganjil, banyak nomor rumah yang sanggup dibuat adalah ....
A. 405
B. 250
C. 225
D. 150
E. 125
Pembahasan Nomor 28
29. Pada pelemparan tiga keping mata uang logam yang dilempar sebanyak 40 kali, frekuensi cita-cita muncul ketiga sisi pada keping uang logamnya angka yaitu . . ..
A. 5
B. 10
C. 15
D. 20
E. 25
30. Diagram berikut memperlihatkan tingkat pendidikan karyawan suatu perusahaan.
Persentase karyawan yang berpendidikan SMK yaitu ....
A. 23,4%
B. 24,5%
C. 24,7%
D. 32,4 %
E. 35,7%
Pembahasan Nomor 30
31. Perhatikan data pada tabel berikut.

Median dari data pada tabel di atas yaitu . . . .
A. 70,21
B. 71,21
C. 73,21
E. 77,21
D. 74,21
Pembahasan Nomor 31
Kuartil ketiga dari data tersebut yaitu . . . .
A. 152,5 rnm
B. 153,8 mm
c. 154,3 rnm
D. 156,7 mm
E. 157,3 rnm
Pembahasan Nomor 32
Pembahasan Nomor 3
4. Jika 2log 3 = a dan 2log 5 = b, nilai 2log 135 yaitu ....
A. 3(a + b)
B. 3a + b
C. a+ 3b
D. a3 + b
E. a+ b3
Pembahasan Nomor 4
5. Untuk membeli 3 benda A dan 4 benda B Ria membayar Rp19.000,00; sedangkan untuk membeli 2 benda A dan 7 benda B Ria membayar Rpl 7.000,00. Jika Ria membeli
4 benda A dan 8 benda B, Ria harus membayar ....
A. Rp 18.000,00
B. Rp 19.500,00
C. Rp 20.000,00
D. Rp24.000,00
E. Rp28.000,00
Pembahasan Nomor 5
6. Diketahui persamaan garis 2x - y = 5 dan 3x - y = 2. Persamaan garis yang melalui titik potong kedua garis tersebut dan sejajar garis y - 3x = 2 yaitu ....
A y = 3x + 2
B. y = 3x - 5
C. y = 3x - 2
D. y = 13x + 5
E. y = - 13x - 6
Pembahasan Nomor 6
7. Grafik dari fungsi kuadrat f(x)= 3x2 + 7x - 6 yaitu .
Pembahasan Nomor 7
8. Seorang penjahit memiliki 60 m kain wol dan 100 m kain katun yang akan dibentuk dua model seragam. Seragam model A memerlukan 3 m kain wol dan 1 m kain katun , sedangkan seragam model B memerlukan 2 m kain wol dan 2 m kain katun. Misalkan banyak seragam model A adalah x dan banyak seragam model B yaitu y, model
matematika dari permasalahan tersebut yaitu . . . .
A. 3x + y < 2x + 2y < 100; x > 0; y > 0B. 3x + 2y < 60; x + 2y < 100; x > 0; y > 0
C. 3x + 2y < 100; x + 2y < 60; x > 0; y > 0
D. 2x + 3y < 60; 2x + 2y < 100; x > 0; y > 0
E. 2x + 3y < 100; 2x + 2y < 60; x > 0; y > 0
Pembahasan Nomor 8
9. Daerah yang diarsir pada gambar di samping merupakan penyelesaian suatu sistem pertidaksamaan linear.

Sistem pertidaksamaan linear yang memenuhi adalah
A. x + 4y > 4; 4x + 3y < 12; x > 0; y > 0
B. x + 4y > 4; 3x + 4y < 12; x > 0; y > 0
C. x + 4y < 4; 3x + 4y < 12; x > 0; y > 0
D. 4x + y < 4; 4x + 3y < 12; x > 0; y > 0
E. 4x + y < 4; 3x + 4y < 12; x > 0; y > 0
Pembahasan Nomor 9
10. Diketahui sistem pertidaksamaan x + 4y < 14; 3x + 2y < 12; x > 0; y > 0. Nilai maksimum z = 4x + 5y untuk x dan y pada tempat penyelesaian sistem pertidaksamaan tersebut yaitu . . ..
A. 15
B. 16
C. 23
D. 30
E. 56
Pembahasan Nomor 10

Pembahasan Nomor 11
Soal dan Pembahasan Nomor 12
A. 0°
B. 45°
C. 60°
D. 120°
E. 135°
Pembahasan Nomor 13
14. Ingkaran dari pemyataan "Jika batas nilai kelulusan tinggi, maka beberapa siswa gagal ujian" yaitu ...
A. Jika batas nilai kelulusan tidak tinggi, maka beberapa siswa lulus ujian.
B. Jika batas nilai kelulusan tidak tinggi, maka beberapa siswa tidak gagal ujian.
C. Jika beberapa siswa tidak gagal ujian, maka batas nilai kelulusan tidak tinggi.
D. Batas nilai kelulusan tinggi tetapi semua siswa tidak gagal ujian.
E. Batas nilai kelulusan tidak tinggi dan semua siswa tidak gagal ujian.
Pembahasan Nomor 14
15. Kontraposisi dari pemyataan: "Jika x2 - 0,04 > 0, maka x < -0,2 atau x > 0,2" yaitu ...
A. Jika x < -0,2 atau x > 0,2, maka x2 - 0,04 > 0.
B. Jika -0,2 < x < 0,2, maka x2 - 0,04 < 0.
C. Jika -0,2 < x < 0,2, maka x2 - 0,04 < 0.
D. Jika x2 - 0,04 < 0, maka -0,2 < x < 0,2.
E. Jika x2 - 0,04 < 0, maka x < -0,2 dan x > 0,2.
Pembahasan Nomor 15
16. Diketahui permis-premis sebagai berikut.
Premis 1: Jika seorang siswa kreatif, maka ia akan sekolah di SMK.
Premis 2: Jika seorang siswa sekolah di SMK, maka ia dapat bekerja atau kuliah.
Premis 3: I wan seorang siswa yang tidak bekerja dan tidak kuliah.
Kesimpulan dari premis-premis di atas yaitu ...
A. lwan seorang siswa kreatif.
B. Iwan bukan seorang siswa yang sekolah di SMK.
C. Iwan seorang siswa yang bekerja.
D. Iwan seorang siswa yang sekolah di SMK.
E. Iwan seorang siswa yang tidak kreatif.
Pembahasan Nomor 16
17. Perhatikan gambar berikut.

Garis pelukis pada bangkit kerucut di atas ditunjukkan dengan abjad . . . .
A. a
B. b
C. c
D. d
E. e
Pembahasan Nomor 17
18. Perhatikan gambar desain komponen elektro berikut.

Luas permukaan yang tampak pada gambar di atas adalah
A. 98 cm2
B. 116 cm2
c. 175 cm2
D. 224 cm2
E. 274 cm2
Pembahasan Nomor 18
19. Diketahui balok dengan ukuran panjang 20 cm, lebar 15 cm, dan tinggi 8 cm. Luas permukaan balok tersebut adalah ....
A. 240 cm2
B. 320 cm2
C. 600 cm2
D. 1.160 cm2
E. 2.000 cm2
Pembahasan Nomor 19
20. Sebuah tabung tertutup akan dibentuk dari selembar seng dengan jari-jari 28 cm dan tinggi 45 cm. Luas seng yang dibutuhkan untuk menciptakan tabung tersebut yaitu . . . .
A. 4.928 cm2
B. 5.720 cm2
C. 7.920 cm2
D. 9.840 cm2
E. 12.848 cm2
Pembahasan Nomor 20
21. Diketahui prisma dengan bantalan segitiga ketiga sisi berukuran 5 cm, 12 cm, dan 13 cm. Jika tinggi prisma 10 cm, volume prisma tersebut yaitu . . . .
A. 144 cm3
B. 169 cm3
C. 200 cm3
D. 225 cm3
E. 300 cm3
Pembahasan Nomor 21
22. Suatu segitiga ABC dengan panjang sisi AC = 18 cm, B= 60°, dan A = 75°. Panjang sisi AB yaitu ....
A. 3√3
B. 3√6
C. 6√3
D. 6√6
E. 9√6
Pembahasan Nomor 22
23. Koordinat titik P(√24, -2√2) bila diubah ke dalam koordinat polar menjadi ....
A. (4√2, 120°)
B. (4√2, 300°)
C. (4√2, 330°)
D. (6, 300°)
E. (6, 330°)
Pembahasan Nomor 23
24. Seorang pengusaha mengurutkan banyak unit barang yang dihasilkannya. Temyata banyak barang yang diproduksi pada tiap bulan sebanyak (25n + 50) unit dengan n
menyatakan bulan (n = 1, 2, 3, ... , 10). Jumlah barang yang diproduksi selama sepuluh bulan yaitu . . ..
A. 2.000 unit
B. 1.950 unit
C. 1.900 unit
D. 1.875 unit
E. 1.825 unit
Pembahasan Nomor 24
25. Jumlah bilangan orisinil antara 1 hingga 100 yang habis dibagi 3 yaitu ....
A. 1.263
B. 1.683
C. 1.789
D. 1.883
E. 1.938
Pembahasan Nomor 25
26. Suku pertama dan kelima dari suatu deret geometri berturut turut adalah 5 dan 80. Jumlah 4 suku pertama dari deret geometri tersebut yaitu . . . .
A. 5
B. 10
C. 25
D. 75
E. 155
Pembahasan Nomor 26
27. Jumlah tak hingga dan suku pertama dari suatu deret geometri berturut-turut yaitu 16 dan 8. Rasio deret tersebut adalah ....
A. 1/4
B. 2/4
C. 3/4
D. 1
E. 5/4
Pembahasan Nomor 27
28. Sebuah nomor rumah terdiri dari tiga angka. Jika angka pertama dan terakhir dari nomor rumah tersebut adalah angka ganjil, banyak nomor rumah yang sanggup dibuat adalah ....
A. 405
B. 250
C. 225
D. 150
E. 125
Pembahasan Nomor 28
29. Pada pelemparan tiga keping mata uang logam yang dilempar sebanyak 40 kali, frekuensi cita-cita muncul ketiga sisi pada keping uang logamnya angka yaitu . . ..
A. 5
B. 10
C. 15
D. 20
E. 25
Pembahasan Nomor 29
30. Diagram berikut memperlihatkan tingkat pendidikan karyawan suatu perusahaan.
Persentase karyawan yang berpendidikan SMK yaitu ....
A. 23,4%
B. 24,5%
C. 24,7%
D. 32,4 %
E. 35,7%
Pembahasan Nomor 30
31. Perhatikan data pada tabel berikut.

Median dari data pada tabel di atas yaitu . . . .
A. 70,21
B. 71,21
C. 73,21
E. 77,21
D. 74,21
Pembahasan Nomor 31
32. Perhatikan data pada tabel berikut.
A. 152,5 rnm
B. 153,8 mm
c. 154,3 rnm
D. 156,7 mm
E. 157,3 rnm
Pembahasan Nomor 32
Soal dan Pembahasan Nomor 33
Soal dan Pembahasan Nomor 34
Soal dan Pembahasan Nomor 35
Soal dan Pembahasan Nomor 36
Soal dan Pembahasan Nomor 37
Soal dan Pembahasan Nomor 38
Soal dan Pembahasan Nomor 39
Soal dan Pembahasan Nomor 40












































Posting Komentar untuk "Latihan Soal Dan Pembahasan Un/Unbk Matematika Smk 2019"